Číselná soustava nebo řada existovala s prvními počty. K prastarým příběhům však patří historie nuly, která vznikla až mnohem později. Pro nás je však zcela přirozená.
V dávné minulosti ale nejen, že nulu nepoužívali. Tento prostý znak byl cosi cizího a dokonce obávaného. Proto se četné kultury rozhodly, že se bez ní raději obejdou. Její základní vlastností je totiž skutečnost, že v běžném životě ji prakticky nepotřebujeme. Nechodíme si koupit nula cibule, vždycky pracujeme s počtem. Svým způsobem jde o nejjemnější číslo, které má ovšem zajímavou moc. Cokoli se s ní totiž setká, čeká rozpad.
Matematika na praktické věci
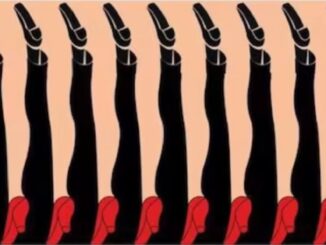
Na vyjádření absence vlastnictví nebylo potřeba zvláštní číslo. Proto se nezdálo nutné vyjadřovat, že něco neexistuje. Umění počítat bylo v dávnověku dar téměř mystický. Bylo na stejné úrovni jako čarování nebo oslovování bohů skrze obřady. Egyptská kniha mrtvých dokonce uvádí, že převozník duší Agen nepustil na onen svět nikoho, kdo si neuměl spočítat vlastní prsty. Řecký Charón zase požadoval platbu mincí. Kdepak se nám na obrázku schovává číslo 9?


Univerzální optická hádanka pro vysoké školy zaznamenala šílenou 4% úspěšnost
Například matematici Egypta byli slavní po celém Středomoří. I tak ale nemáme jediný doklad o tom, že by používali nulu. Pravděpodobně hrálo roli i to, že jejich matematika zpracovávala hlavně praktické problémy. Výborně počítali dny a čas, měřili objemy, hranicí jejich schopností však bylo násobení. Matematika tu nefigurovala jako teoretická věda, možná malou výjimkou v astrologii.
Abstrakce a systém Mayů
Nestalo se tak ani u Řeků, kteří se naopak teorii věnovali hodně. Poprvé nalézáme nulu ve spisech babylonských matematiků z doby asi 300 let před Kristem. Nebyla to však skutečná číselná hodnota, jen značka pro prázdny prostor v zápisu. Nezávislé na Babylonu ji však objevili i tajemní Mayové. Ale jestli stále tápete v dnešním rébusu, tady vám neseme jeho řešení.

Plné početní využití nuly coby čísla pochází z Indie kolem roku 458. jestli ji odečteme nebo přidáme, číslo se nezmění. Při násobení ale číslo mizí a dostáváme opět nulu.